Science Assessment ~ Topics ~ Energy: Forms, Transformation, Transfer, and Conservation ~ Item RG179001 ~ Student Performance

A person drops a rock off of a cliff, which is 100 meters high. As the rock falls, its speed increases, and its mass stays the same.

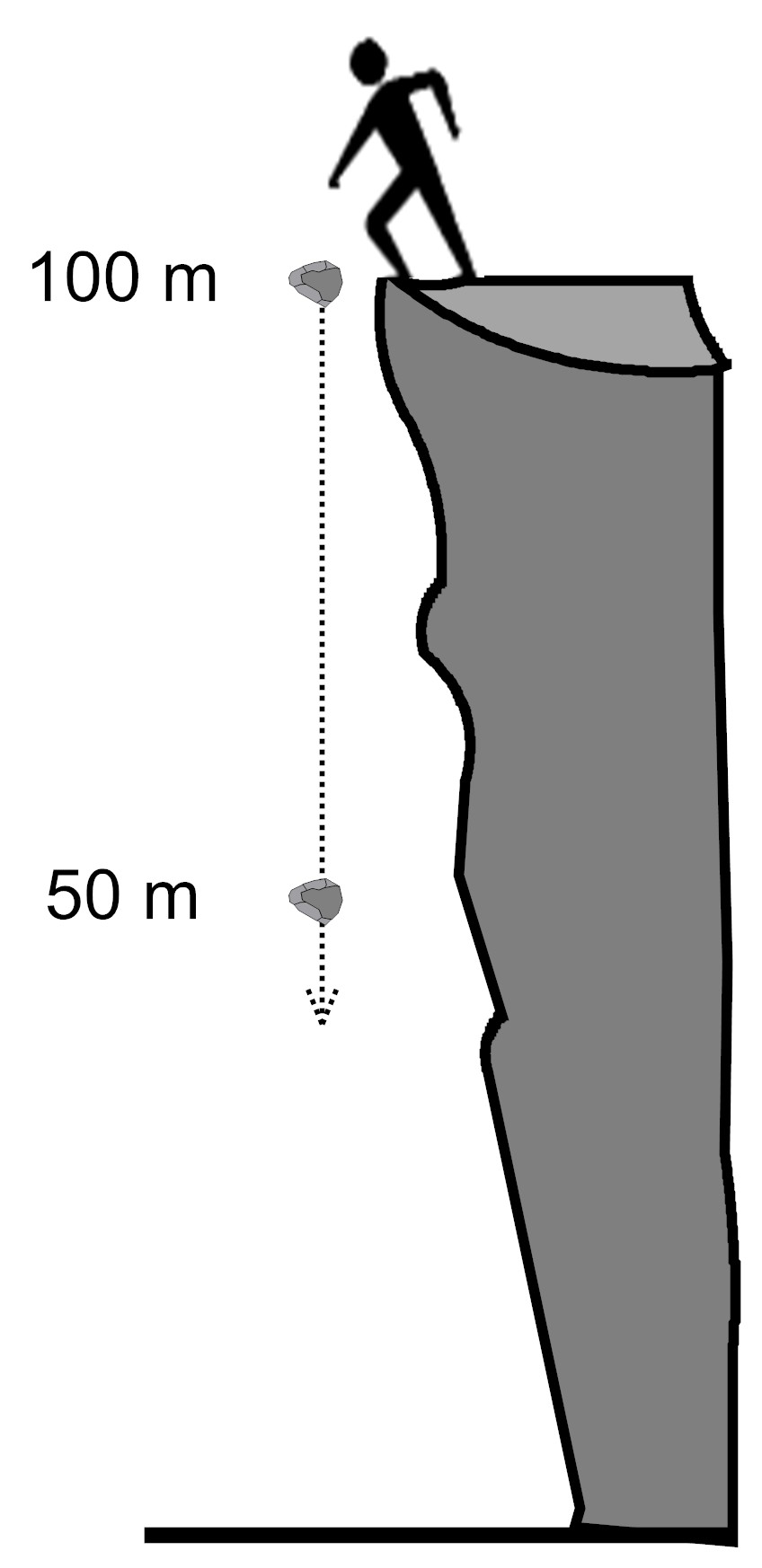
How does the gravitational potential energy of the rock change from the point at which the person drops it to the point at which it is 50 meters above the ground?

The gravitational potential energy of the rock at 50 meters is double the gravitational potential energy at 100 meters because the amount of gravitational potential energy an object has is inversely proportional to the height the object is above the ground.
The gravitational potential energy of the rock at 50 meters is half of the gravitational potential energy at 100 meters because the amount of gravitational potential energy an object has is directly proportional to the height the object is above the ground.
The gravitational potential energy of the rock at 50 meters is the same as the gravitational potential energy at 100 meters because the amount of gravitational potential energy an object has depends only on the mass of the object, and the mass stayed the same.
The gravitational potential energy of the rock at 50 meters is zero because gravitational potential energy is the potential to fall; therefore, the rock lost its gravitational potential energy when it was dropped.

Distribution of responses
Answer Choice	Overall	Grades			Gender		Primary Language
	n = 7092	4–5 n = 0	6–8 n = 4092	9–12 n = 3000	Male n = 3397	Female n = 3541	English n = 6131	Other n = 769
A.	34%	N/A	35%	32%	34%	34%	34%	31%
B.	32%	N/A	30%	35%	33%	32%	32%	32%
C.	23%	N/A	23%	23%	23%	23%	23%	26%
D.	11%	N/A	11%	10%	11%	11%	10%	11%

Science Assessment

Item RG179001: The gravitational potential energy of a falling rock at 50 meters is half of the gravitational potential energy at 100 meters because the amount of gravitational potential energy an object has is directly proportional to the height the object is above the ground.