ASPECt
Energy: Forms, Transformation, Transfer, and Conservation
Item RG003003: Kinetic energy is proportional to the speed squared, so when a moving object has its speed increased by two the kinetic energy of that object increases by four.
A person drops a rock off of a cliff. As the rock falls, its speed increases, and its mass stays the same. The person determined the speed of the rock at two time points. At Time 1, the rock was falling at 20 meters per second. At Time 2, the rock was falling at 40 meters per second.
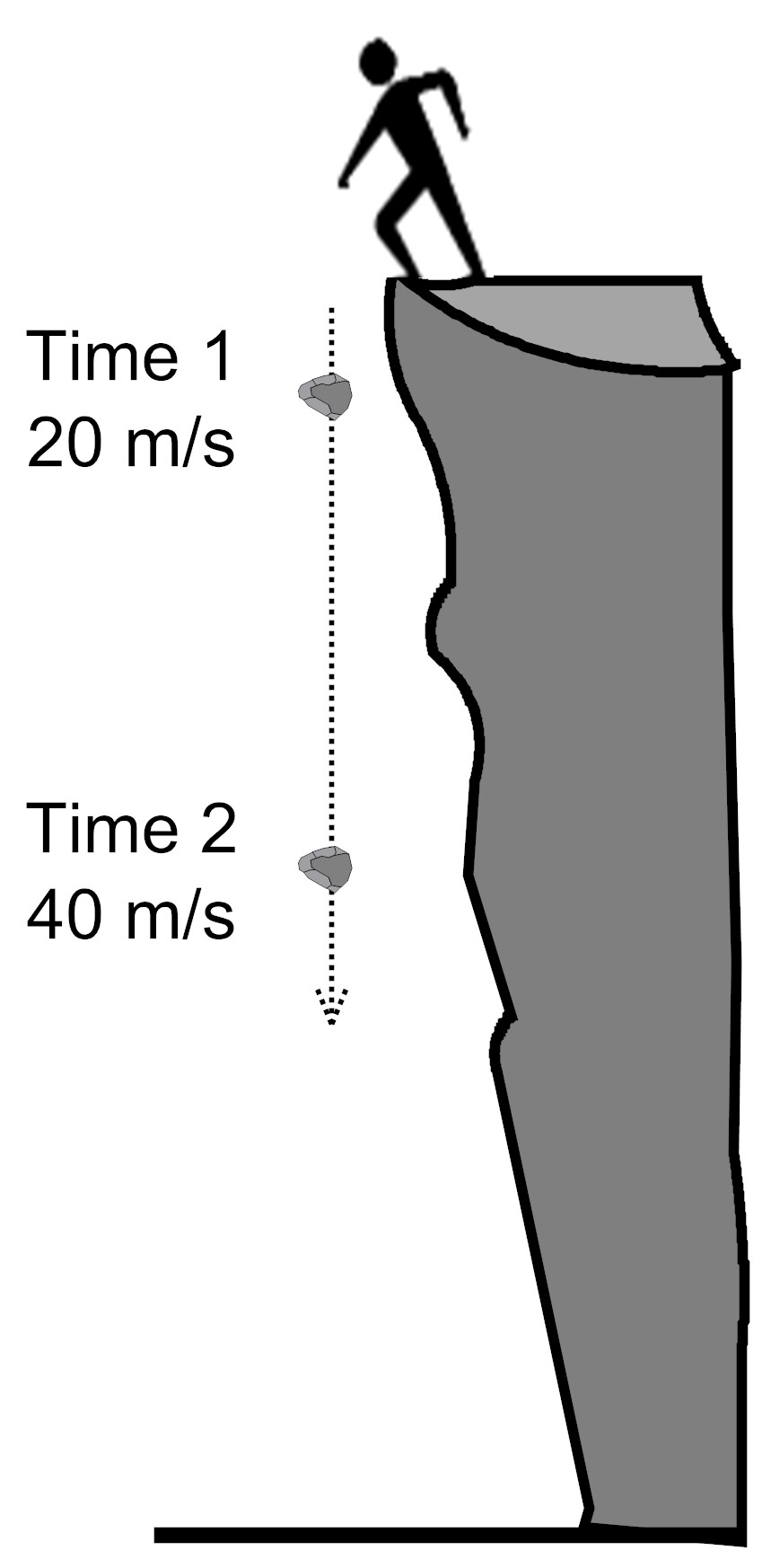
How does the kinetic energy (motion energy) of the rock change from Time 1 to Time 2?
- The kinetic energy of the rock at Time 2 is half of the kinetic energy at Time 1 because the amount of kinetic energy an object has is inversely proportional to its speed.
- The kinetic energy of the rock at Time 2 is double the kinetic energy at Time 1 because the amount of kinetic energy an object has is directly proportional to its speed.
- The kinetic energy of the rock at Time 2 is four times the kinetic energy at Time 1 because the amount of kinetic energy an object has is directly proportional to the square of its speed.
- The kinetic energy of the rock at Time 2 is the same as the kinetic energy at Time 1 because the amount of kinetic energy an object has does not depend on its speed.
Answer Choice |
Overall |
Grades |
Gender |
Primary Language |
||||
|---|---|---|---|---|---|---|---|---|
| n = 1115 |
4–5 n = 0 | 6–8 n = 575 |
9–12 n = 540 |
Male n = 555 |
Female n = 534 |
English n = 981 |
Other n = 105 |
|
| A. | 20% | N/A | 23% | 17% | 20% | 20% | 20% | 23% |
| B. | 61% | N/A | 60% | 63% | 59% | 64% | 62% | 60% |
| C. | 11% | N/A | 9% | 14% | 13% | 8% | 11% | 9% |
| D. | 7% | N/A | 8% | 7% | 8% | 7% | 7% | 9% |